-
Bug
-
Resolution: Out of scope
-
P2: Important
-
None
-
5.12, 5.15.0 RC
-
Desktop
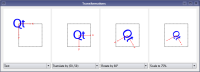
QTransform Rot = QTransform().rotate(90); QTransform ScaleX = QTransform().scale(2,1); QPointF Pt_Rot = Rot.map(QPointF(1,0)); // returns (0,1) , ok as (mathematically) expected QPointF Pt_RotThenScaleX = ScaleX.map(Pt_Rot); // returns (0,1) , ok as (mathematically) expected QTransform RotThenScaleX = Rot.scale(2,1); QPointF Pt_RotThenScaleX_2 = RotThenScaleX.map(QPointF(1,0)); // (0,2) ! Unexpected - Its actually scaled (x) first, then rotated qDebug()<< "Pt_RotThenScaleX: " << Pt_RotThenScaleX; qDebug()<< "Pt_RotThenScaleX_2: " << Pt_RotThenScaleX_2;
Output:
Pt_RotThenScaleX: QPointF(0,1) Pt_RotThenScaleX_2: QPointF(0,2)
I would expect both Pt_RotThenScaleX, and Pt_RotThenScaleX_2 to be
"QPointF(0,1)"
Its not because multiplying QTransforms and then applying the product to a
vector is effectively applying the QTransforms in the reverse order to the
vector.
Let
S be one (eg a Matrix for a scale)
R be another Matrix (eg for a rotation)
V be a vector (eg point in a 2d space such as QPointF(1,0) above)
Then mathematically S x R x V should be applied as S x ( R x V).
ie R applied first then S.
Qt is internally turning "SxR" into "RxS" before
multiplying it by V (Pt_RotThenScaleX_2 above)
In above code, expectation is that Scaling is done first, analogous to the Matrix multiplication (which is performed right to left on the vector they're operating on) that these Transforms represent. But the actual order performed is the opposite.
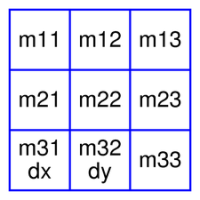
Formula used as documented also is faulty : https://bugreports.qt.io/browse/QTBUG-83869